이 포스팅은 아래의 영문 페이지를 우리말로 옮긴 것이다. 머신러닝에 대해 공부하던 중 예제 중심으로 가장 잘 설명이 되어 있는 것으로 보여 복습도 할 겸 나중에 쉽게 찾아볼 수 있도록 우리말로 옮겨두려고 한다. 전부 옮기진 않고 옮기고 싶은 부분만 옮겼으며, 중간중간 박스로 부연 설명을 했다.
Fraud Detection with Python
Compare SMOTE to original data¶ In the last exercise, you saw that using SMOTE suddenly gives us more observations of the minority class. Let's compare those results to our original data, to get a good feeling for what has actually happened. Let's have a
trenton3983.github.io
목차
시작하기에 앞서 필요한 라이브러리를 불러오고 예제 파일을 사용하기 위한 코드를 작성한다.


1. 개요와 데이터 준비
부정탐지에 관한 일반적인 문제와 데이터를 리샘플링하는 방법과 불균형 데이터 문제를 해결하는 방법을 알아보자.
1.1.1 부정거래 비율 확인하기
이 장에서는 신용 카드 거래 데이터(creditcard_sampledata.csv)를 다룬다. 다행히 부정거래는 극소수이다.
그러나 머신러닝 알고리즘은 일반적으로 데이터 세트에 포함된 클래스들이 거의 균등할 때 가장 잘 작동한다. 부정거래가 적다면 이를 식별하는 방법을 배울 데이터가 거의 없는 것이다. 이를 클래스 불균형(class imbalance)이라고 하며 부정 탐지를 할 때의 주요 도전 과제 중 하나이다.
| ※ 여기에서는 부정거래와 정상거래가 클래스가 된다. 머신러닝을 부정탐지에 사용하려는 경우, 보통은 부정사례의 개수가 너무 적기 때문에 학습 데이터가 부족해서 머신러닝 알고리즘이 잘 작동하지 않는다는 말이다. |
데이터 세트를 탐색하고 클래스 불균형 문제를 살펴보자.
- 신용 카드 데이터를 df에 할당한다.

- .info()와 .head()를 사용하여 df에 대한 정보를 출력한다.

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 5050 entries, 0 to 5049
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Unnamed: 0 5050 non-null int64
1 V1 5050 non-null float64
2 V2 5050 non-null float64
3 V3 5050 non-null float64
4 V4 5050 non-null float64
5 V5 5050 non-null float64
6 V6 5050 non-null float64
7 V7 5050 non-null float64
8 V8 5050 non-null float64
9 V9 5050 non-null float64
10 V10 5050 non-null float64
11 V11 5050 non-null float64
12 V12 5050 non-null float64
13 V13 5050 non-null float64
14 V14 5050 non-null float64
15 V15 5050 non-null float64
16 V16 5050 non-null float64
17 V17 5050 non-null float64
18 V18 5050 non-null float64
19 V19 5050 non-null float64
20 V20 5050 non-null float64
21 V21 5050 non-null float64
22 V22 5050 non-null float64
23 V23 5050 non-null float64
24 V24 5050 non-null float64
25 V25 5050 non-null float64
26 V26 5050 non-null float64
27 V27 5050 non-null float64
28 V28 5050 non-null float64
29 Amount 5050 non-null float64
30 Class 5050 non-null int64
dtypes: float64(29), int64(2)
| ※ 데이터를 보면 열제목은 V1~V28로 되어 있고, 값들도 일정 범위의 숫자 데이터로 되어 있다. 머신러닝에 활용하기 위하여 정규화된 데이터인 것이다. 신용카드 데이터에는 개인정보가 다수 포함되어 있다는 것도 이러한 데이터 가공의 목적의 하나가 될 것이다. 한편, Amount는 거래 금액이고, Class는 0 또는 1로서 부정거래 여부를 표시하는 열이다. |
- .value_counts()를 사용하여 'Class' 열에서 부정거래와 정상거래의 수를 가져와 결과를 occ에 할당한다.
- 총 거래수 대비 부정거래 비율을 출력한다.

부정거래의 비율이 매우 낮은 클래스 불균형에 해당한다. 다음으로 이를 처리하는 방법을 알아보자.
1.1.2 데이터 시각화
앞에서 부정거래 비율이 매우 낮다는 것을 알아보았다. 이에 대해 데이터 리샘플링 등의 조치를 할 수 있다.
여기에서는 데이터를 살펴보고 부정거래 비율을 시각화한다. 데이터를 변경하기 전에 먼저 데이터를 살펴보는 것이 좋은 출발점이다.
시각화를 통해 우리가 심하게 불균형한 데이터를 다루고 있다는 것을 분명하게 보여줄 수 있다.
- X와 y의 산점도 그래프를 그리기 위하여 plot_data(X, y) 함수를 정의

- df에서 prep_data() 함수를 사용하여 X와 레이블 y를 생성


- X 및 y에 대해 plot_data() 함수를 실행하여 결과를 시각화

데이터를 시각화하면 부정거래가 어떻게 흩어져 있는지, 얼마나 적은 부정거래가 있는지 즉시 확인할 수 있다.
다음으로 부정거래 비율을 개선하는 방법을 시각적으로 살펴본다.
1.2 데이터 리샘플링을 통한 부정거래 탐지 개선
리샘플링은 데이터 세트가 불균형한 경우 모델 성능에 도움이 될 수 있다.
1.2.0.1 언더샘플링 / 1.2.0.2 오버샘플링
- 다수(정상거래) 클래스의 언더샘플링
- 불균형 데이터를 조정하는 간단한 방법
- 부정거래 사례에 맞추기 위해서 정상거래 샘플에서 무작위로 추출(그림 참조) - 소수(부정거래) 클래스의 오버샘플링
- 부정거래 샘플에서 무작위 추출하고 이를 복사해 부정거래 샘플의 양을 늘림(그림 참조) - 두 가지 방법 모두 부정거래와 정상거래 간의 균형을 유지
- 단점
- 언더샘플링을 사용하면 많은 정보가 버려짐
- 오버샘플링을 사용하면 모델이 많은 중복 샘플을 학습함
1.2.0.3 파이썬의 imblearn 모듈을 활용한 리샘플링 기법
사이킷럿과 호환이 된다.
from imblearn.over_sampling import RandomOverSampler
method = RandomOverSampler()
X_resampled, y_resampled = method.fit_sample(X, y)
compare_plots(X_resampled, y_resampled, X, y)
더 짙은 파란 점들이 중복 샘플이 많음을 나타낸다.(그림 참조)
| ※ 오버샘플링 방법을 이용함으로써 중복 샘플이 생성되어 원래의 그래프에 비해 점이 진하게 표시된다. |
1.2.0.4 SMOTE
- Synthetic minority Oversampling Technique (SMOTE)
- 불균형 데이터 세트에 대한 리샘플링 전략
- 소수 클래스를 오버샘플링하여 불균형을 조정하는 또 다른 방법
- SMOTE는 부정거래의 가장 최근접 이웃의 특성을 사용하여 새로운 부정거래 샘플을 만듦(그림 참조)
- 중복 샘플을 하지 않음
1.2.0.5 최적의 리샘플링 기법을 선택하는 것은 상황에 따라 다름
- 무작위 언더샘플링(RUS):
- 데이터가 많고 소수 사례가 많으면 언더샘플링이 계산상 더 편리
- 대부분의 경우 데이터를 버리는 것은 바람직하지 않음 - 무작위 오버샘플링(ROS):
- 직관적
- 중복 샘플로 모델 학습 - SMOTE:
- 더 세련됨
- 현실적인 데이터 세트
- 합성 데이터로 학습
- 소수 사례의 특징이 유사한 경우에만 잘 작동(부정사례가 퍼져 있고 분명하지(distinct) 않은 경우 최근접 이웃이 부정사례가 아닐 수 있으므로 데이터에 노이즈가 발생)
1.2.0.6 언제 리샘플링을 사용하는가
- 테스트 세트가 아니라 훈련 세트에 리샘플링 사용
- 목표는 균형 잡힌 데이터를 제공하여 더 나은 모델을 만드는 것임
- 합성 샘플을 예측하는 것이 목표가 아님 - 테스트 데이터에는 중복 및 합성 데이터가 없어야 함
- 실제 데이터에서만 모델을 테스트함
1.2.1 불균형한 데이터를 위한 리샘플링 기법
ROS 및 SMOTE를 사용하면 소수 클래스에 더 많은 사례를 추가한다.
RUS는 다수 클래스를 줄여 데이터 균형을 조정한다.
1.2.2 SMOTE 기법 적용하기
여기에서는 SMOTE(Synthetic Minority Over-sampling Technique)를 사용하여 데이터 균형을 조정한다. ROS와 달리 SMOTE는 동일한 사본을 생성하지 않고 소수 클래스의 샘플과 매우 유사한 새로운 합성 샘플을 생성한다. 따라서 SMOTE가 약간 더 정교하므로 SMOTE를 신용 카드 데이터에 적용해 본다.
아래에서는 SMOTE의 효과를 보기 위하여 결과를 시각화하고 원본 데이터와 비교해 본다.
- df에서 prep_data 함수를 사용하여 X와 y를 생성

- SMOTE를 리샘플링 방법으로 하고, method 변수로 할당

- X 및 y에 .fit_resample()을 사용하여 리샘플링된 데이터를 획득

- plot_data() 함수를 사용하여 시각화

이제 소수 클래스가 훨씬 더 눈에 띄게 표시된다.
1.2.3 SMOTE와 원본 데이터 비교
원본 데이터와 새 데이터의 숫자를 보고 산점도 그래프를 나란히 표시해보자.
이를 위해 compare_plot() 함수를 사용한다.

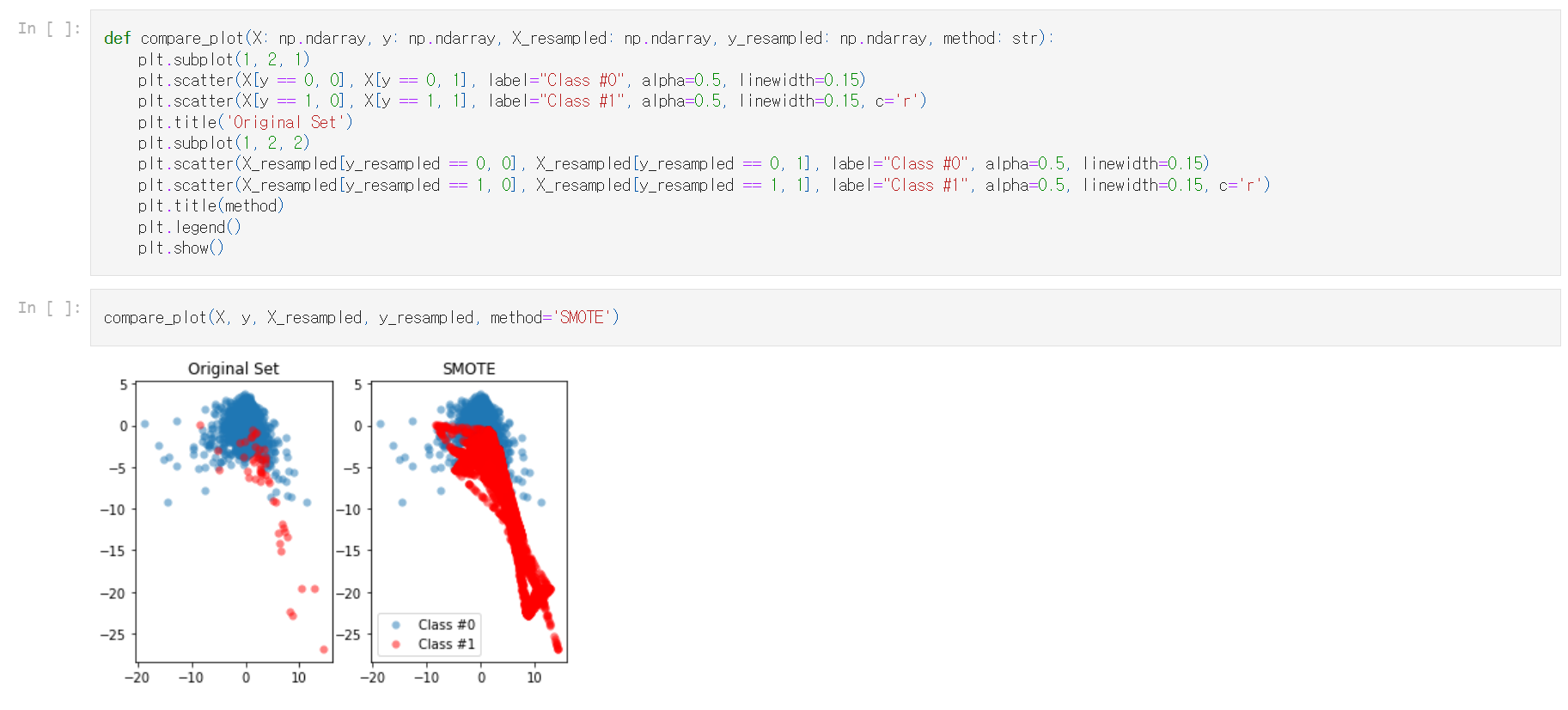
이제 SMOTE가 데이터의 균형을 잡았고 소수 클래스가 다수 클래스와 크기가 동일하다.
다음으로 SMOTE를 구현하는 여러 방법을 보고, 각 방법이 약간 다른 효과를 가지는 것을 살펴본다.
1.3 부정탐지 알고리즘
1.3.0.1 규칙 기반 시스템
- 위험한 우편번호 차단
- 너무 잦은 카드 거래 차단(예: 최근 30분)
- 부정거래를 탐지할 수 있지만 오류도 발생함(false positive)
- 제약점:
- 규칙 별로 임계값이 고정되어 있고 임계값을 결정하기 곤란하며. 시간이 지남에 따라 변화하지 않음
- 예/아니오로 제한(ML은 확률을 산출)
- 특징 간의 상호 작용을 포착하지 못함(예, 거래 규모는 거래 빈도와 결합하여야만 중요함)
1.3.0.2 머신러닝 기반 시스템
- 데이터에 적응하여 시간이 지남에 따라 변경 가능
- 기능별 임계값이 아닌 결합된 모든 데이터를 사용
- 확률을 산출
- 일반적으로 더 나은 성능을 보이며, 규칙과 결합할 수 있음
1.3.1 전통적 부정탐지 기법 살펴보기
여기에서는 예전 방식으로 신용 카드 데이터 세트에서 부정거래를 찾아본다.
먼저 일반적인 통계를 사용하여 임계값을 정의하여 부정거래와 정상거래를 구분한다. 그런 다음 이러한 임계값을 사용하여 부정거래를 탐지한다.
임계값은 보통 관측값의 평균값을 보고 결정한다. 먼저 부정거래와 정상거래 간에 평균이 다른지 확인한다. 그런 다음 해당 정보를 사용하여 임계값을 설정한다. 마지막으로 이것이 얼마나 부정거래를 잘 탐지하는지 확인한다.
- groupby()를 사용하여 클래스에서 df를 그룹화하고 특징별 평균을 구함
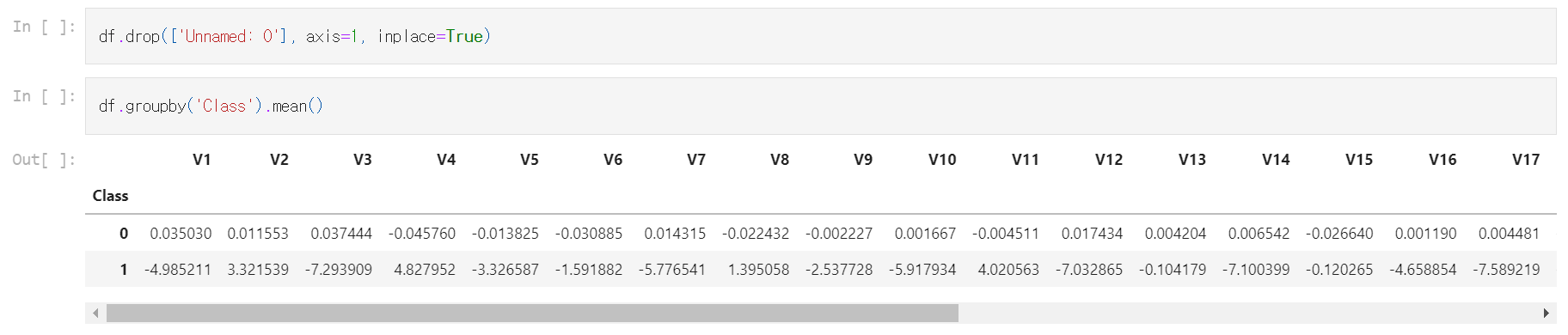
- 부정거래를 표시하기 위하여 V1이 -3보다 작고 및 V3이 -5보다 작은 것을 조건으로 둠

- pandas의 crosstab 함수를 사용하여 표시된 부정거래와 실제 부정거래를 비교

이 규칙을 사용하면 50건의 부정거래 중 22건이 탐지되고 28건은 탐지되지 않으며 16건의 오탐지가 발생한다.
1.3.2 머신러닝 분류를 이용한 부정탐지
여기에서는 신용 카드 데이터에 간단한 머신러닝 모델을 사용해 어떤 일이 발생하는지 살펴본다.
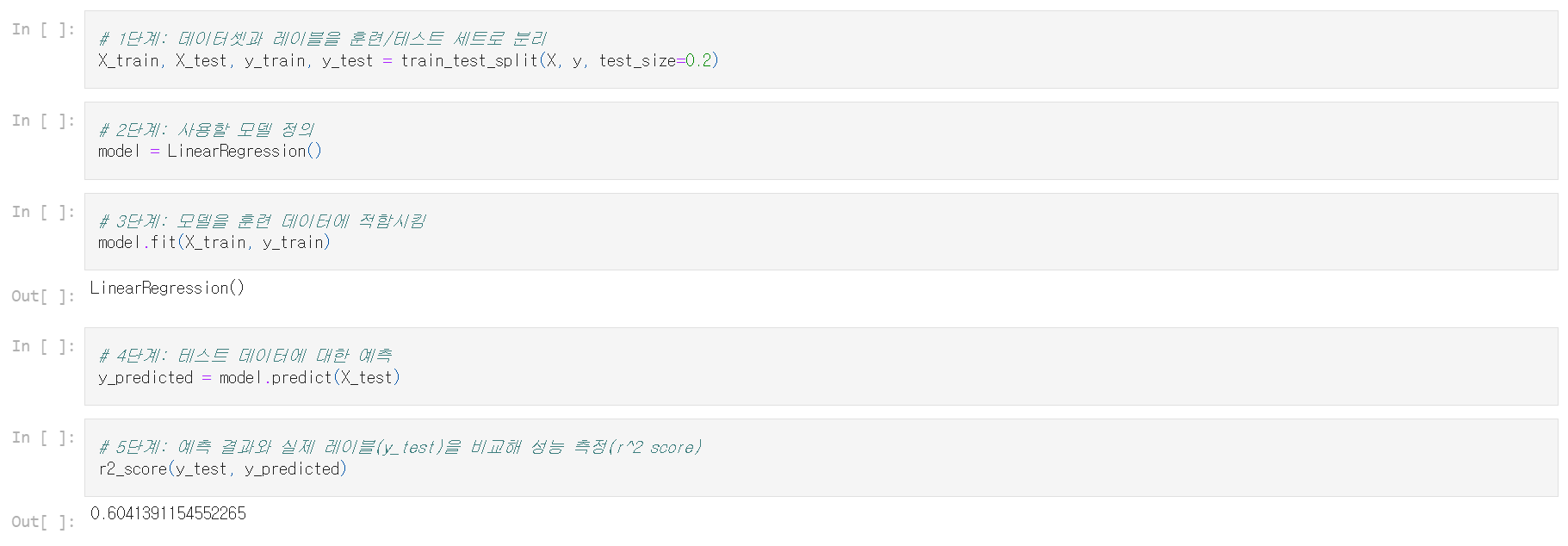
앞서 부정거래 50건 중 22건을 예측했고 16건의 오탐지가 있었다는 것을 염두에 두고 로지스틱 회귀 모델을 구현해 보자.
- X와 y를 훈련 데이터와 테스트 데이터로 분할하고 데이터의 30%를 테스트용으로 둠

- 모델을 훈련 데이터에 적합시킴

- X_test에서 model.predict를 실행하여 예측 결과를 얻음

- y_test와 predicted를 비교하는 혼동 행렬(confusion matrix)로 결과를 확인

결과가 규칙 기반 모델보다 낫다고 생각하는가? 오탐지가 훨씬 적고 부정거래 사례의 비율이 높아져 이전보다 개선되었다.
다음으로는 리샘플링 방법을 사용하여 예측 결과를 더욱 개선할 수 있는지 살펴본다.
1.3.3 SMOTE와 로지스틱 회귀
여기에서는 앞의 로지스틱 회귀 모델을 가져와 SMOTE 리샘플링 방법과 결합한다. 리샘플링 기법과 머신러닝 모델을 한 번에 결합하는 파이프라인을 사용하여 효율적으로 수행하는 방법을 소개한다. 먼저 사용할 파이프라인을 정의한다.

1.3.4 파이프라인
로지스틱 회귀와 SMOTE 방법을 결합하는 파이프라인을 정의했으므로 데이터에서 실행해 보자. 파이프라인을 하나의 머신러닝 모델처럼 취급할 수 있다.
- 데이터 X와 y를 훈련 세트와 테스트 세트로 나눔(테스트 세트를 위해 데이터의 30%를 따로 설정하고 random_state를 0으로 설정)

- 파이프라인을 훈련 데이터에 적합시키고 X_test에 pipeline.predict() 함수를 실행
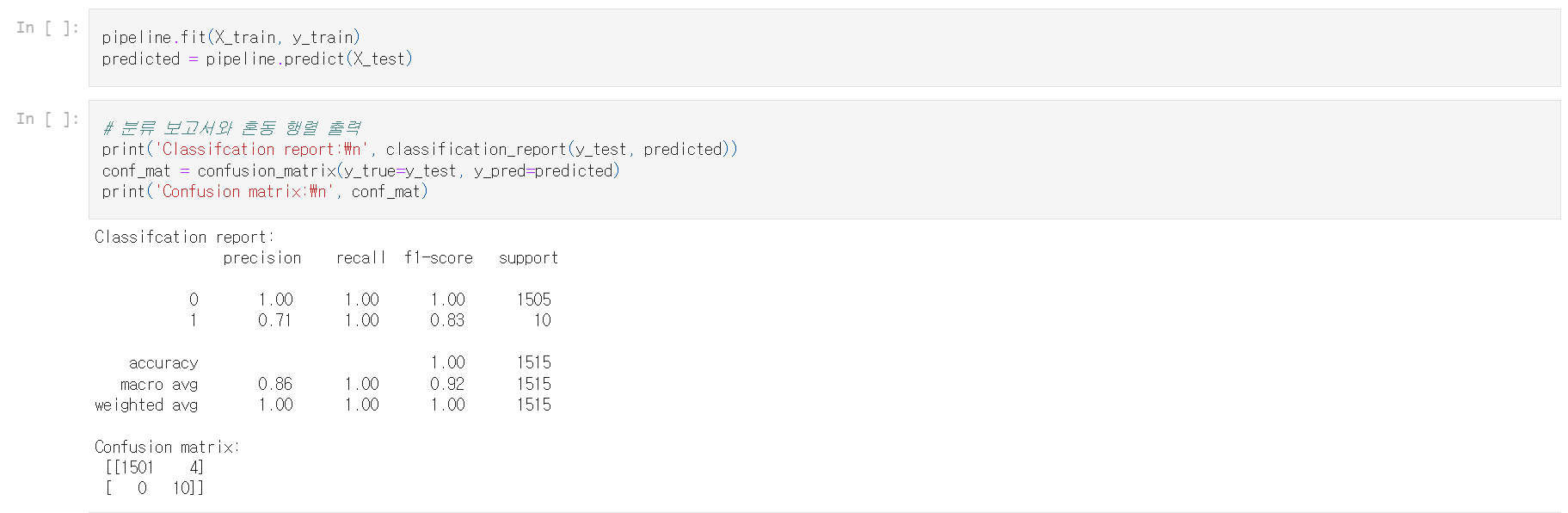
SMOTE가 결과를 약간 개선시켰다. 이제 모든 부정거래를 찾을 수 있지만 오탐지가 4건으로 약간 더 많다. 리샘플링이 반드시 더 나은 결과로 이어지는 것은 아니다. 부정거래 사례가 넓게 흩어져 있는 경우 SMOTE를 사용하면 약간의 편향이 발생할 수 있다.
다음으로는 소수의 부정거래 사례를 더 잘 탐지하기 위해 학습 모델을 조정하는 방법을 알아본다.
2. Labeled Data를 이용한 부정탐지
지도 학습으로 부정거래를 탐지하는 방법을 알아본다.
분류기를 사용하고 조정 및 비교하여 가장 효율적인 부정거래 탐지 모델을 찾는다.
2.1 분류 방법 검토
- 분류: 클래스 분류 데이터(부정거래 여부)가 포함된 훈련 세트를 기반으로 새로운 샘플의 클래스를 식별
- 클래스를 타깃, 레이블이라고도 함
- 이메일 서비스 제공업체의 스팸 탐지는 분류 문제에 해당(스팸과 스팸이 아닌 2개의 클래스만 있으므로 이진 분류)
- 부정 탐지, 환자 진단은 이진 분류 문제이기도 함
- 분류 문제는 일반적으로 yes/no, 1/0 또는 True/False와 같은 범주형 출력을 가짐
2.1.0.1 로지스틱 회귀
로지스틱 회귀는 이진 분류에서 가장 많이 사용되는 머신러닝 알고리즘 중 하나이다.(그림 참조)
불균형한 데이터에 대해 적절하게 조정될 수 있어 부정 탐지에 유용하다.
2.1.0.2 신경망
생략
2.1.0.3 의사결정 트리
- 부정 탐지에 일반적으로 사용됨
- 결과를 쉽게 해석할 수 있음(그림 참조)
- 과적합하는 경향이 있음
2.1.0.4 랜덤 포레스트
- 랜덤 포레스트는 단일 의사결정 트리보다 더 강력함
- 다수의 의사결정 트리를 구성(그림 참조)하고 개별 트리의 최빈 또는 평균 예측 클래스를 출력
- 임의의 특징 하위 집합의 트리 모음으로 구성됨
- 해당 트리들의 예측 결과를 결합하여 최종 예측
- 복잡한 데이터를 처리할 수 있으며 과적합이 발생하지 않음
- 특징 중요도를 보고 해석할 수 있으며, 불균형이 심한 데이터에서 잘 작동하도록 조정 가능
- 계산적으로 복잡하다는 것이 단점
- 부정 탐지에 매우 인기가 있음
2.1.1 자연 적중률
신용 카드 거래 데이터를 다시 사용한다. 먼저 데이터 세트에서 부정거래가 얼마나 많은지 확인해야 한다. 이는 아래에서 사기 탐지를 위한 랜덤 포레스트 분류기를 만들 때 기준 모델의 역할을 한다.
아무것도 하지 않고 전부 정상거래로 예측한다면 95.9%의 확률로 적중한다. 이 숫자보다 낮은 정확도를 얻으면 예측 결과를 개선하지 않는 것이다.
- y의 길이를 구하여 총 샘플 수를 계산함
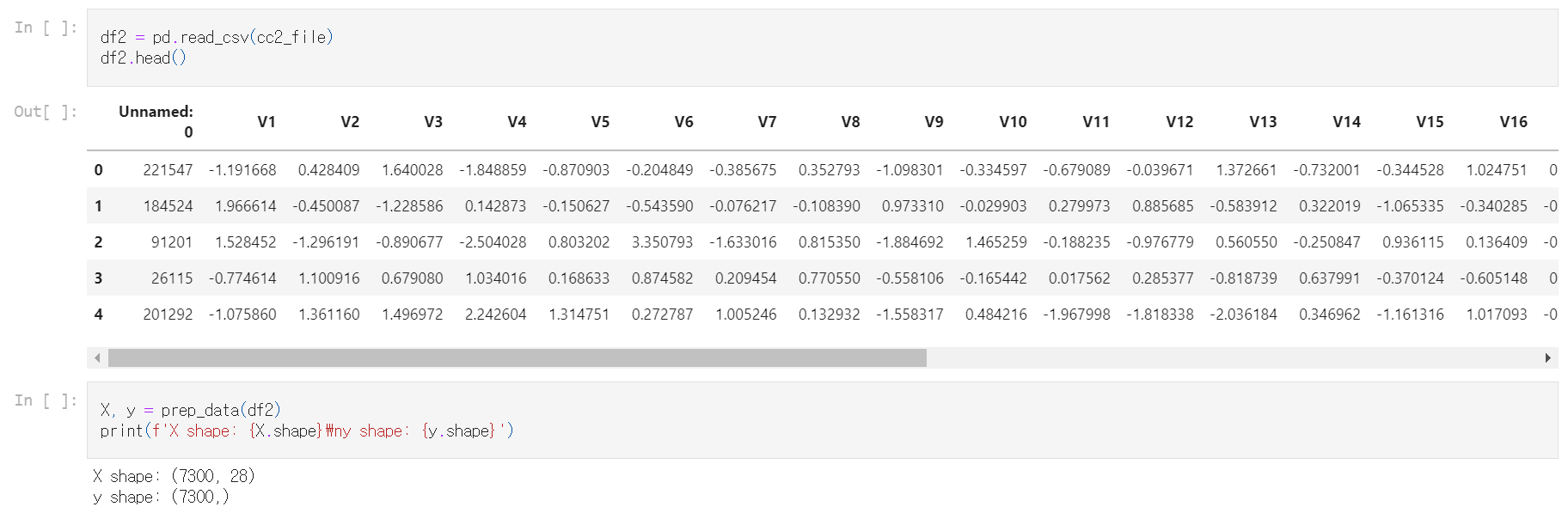

- 리스트 컴프리헨션을 이용해 정상거래 샘플 수를 계산함(y는 NumPy 배열이므로 .value_counts()를 사용할 수 없음)

- 정상거래 샘플 수를 전체 샘플 수로 나누어 자연 정확도를 계산, 백분율을 출력

2.1.2 랜덤 포레스트 분류기
이제 랜덤 포레스트 분류기를 생성해 보자. 먼저 데이터를 테스트 및 훈련 세트로 분할하고 랜덤 포레스트 모델을 정의하는 것으로 시작한다.
- X와 y를 훈련 및 테스트 세트로 분할, 30%의 테스트 세트를 따로 둠
- 랜덤 포레스트 분류기를 모델로 하고 random_state를 5로 함(다른 모델에서 결과를 비교할 수 있으려면 여기에서 random_state를 설정해야 함)

랜덤 포레스트 모델이 특별한 작업 없이 어떻게 수행되는지 보자.
앞서 정의한 모델을 훈련 데이터에 적합시키고 X_test에 대해 예측한다.

실제 데이터인 y_test를 예측 결과와 비교하여 정확도 점수를 출력한다.

랜덤 포레스트는 하위 집합을 사용하여 더 작은 트리를 구축하여 대부분의 경우 과적합을 방지한다.
2.2 성능 평가
2.2.0.1 정확도
정확도는 고도로 불균형한 데이터로 작업할 때 신뢰할 수 있는 성능 평가 방식이 아니다.(그림 참조)
아무것도 하지 않음으로써, 즉 모든 것이 다수 클래스라고 예측함으로써(오른쪽 이미지), 예측 모델을 구축하려고 시도하는 것보다 더 높은 정확도를 얻는다(왼쪽 이미지).
2.2.0.2 혼동 행렬(confusion matrix)(그림 참조)
- FN(false negative): 임신이 아닌 것으로 예측하였지만 실제로는 임신임(모델이 잡히지 않은 부정사례)
- FP(false positive): 임신을 예측하였지만 실제로는 임신하지 않음('오경보' 사례)
- 상황에 따라 FN과 FP 중 무엇이 더 중요한지 결정됨
- 신용 카드 회사는 부정거래로 막대한 비용이 소요될 수 있으므로 가능한 한 많은 부정거래를 포착하고 FN을 줄이기를 원할 수 있음(오경보는 단지 거래가 차단될 뿐임)
- 보험 회사는 많은 오경보를 처리할 수 없음(조사 팀이 투입되기 때문)
- TP, TN는 올바르게 예측된 사례임
2.2.0.3 정밀도와 재현율(precision and recall)
- 신용 카드 회사는 재현율 최적화를 원함
- 보험 회사는 정밀도 최적화를 원함
- 정밀도:
- 예측된 부정거래 중 실제 부정거래의 비율
- TP를 TP와 FP의 합으로 나눈 값 - 재현율:
- 모든 부정거래 중 예측된 부정거래 비율
- TP를 TP와 FN의 합으로 나눈 값 - 정밀도와 재현율은 일반적으로 반비례 관계
2.2.0.4 F-Score
정밀도와 재현율을 모두 측정하며, 정밀도와 재현율 간의 균형을 고려한 성능 측정 항목이다.
2.2.0.5 사이킷런에서 성능 측정 결과 얻기
생략
2.2.0.6 알고리즘을 비교하기 위한 ROC(Receiver Operating Characteristic) 곡선
다양한 임계값 설정에서 FP 비율에 대한 TP 비율을 표시하며, 알고리즘의 성능을 비교하는 데 유용하다.(그림 참조)
2.2.1 랜덤 포레스트 모델 성능 평가
앞서 랜덤 포레스트 모델의 정확도 점수를 계산해 봤고, 부정 탐지의 경우에 정확도 점수는 오해의 소지가 있다는 것을 살펴본 바 있다.
고도로 불균형한 데이터를 사용하는 경우, AUROC 곡선이 다양한 분류기를 비교하는 데 사용되는 보다 안정적인 성능 측정 방법이다.
또한 분류 보고서는 모델의 정밀도와 재현율에 대해 알려 주지만, 혼동 행렬은 실제로 얼마나 많은 부정거래를 올바르게 예측할 수 있는지 보여준다.
- 훈련된 랜덤 포레스트 모델에서 이진 예측을 가져옴

- predict_proba() 함수를 실행하여 예측된 확률을 가져옴

- y_test를 predicted와 비교하여 분류 보고서 및 혼동 행렬을 출력

75건의 부정거래를 예측하고 그중 73건은 실제 부정거래이다. 단 2개의 오탐지가 있다. 매우 높은 정밀도 점수를 얻게 되었으나 실제 부정거래 18건을 놓쳤기 때문에 재현율은 정밀도만큼 좋지 않다.
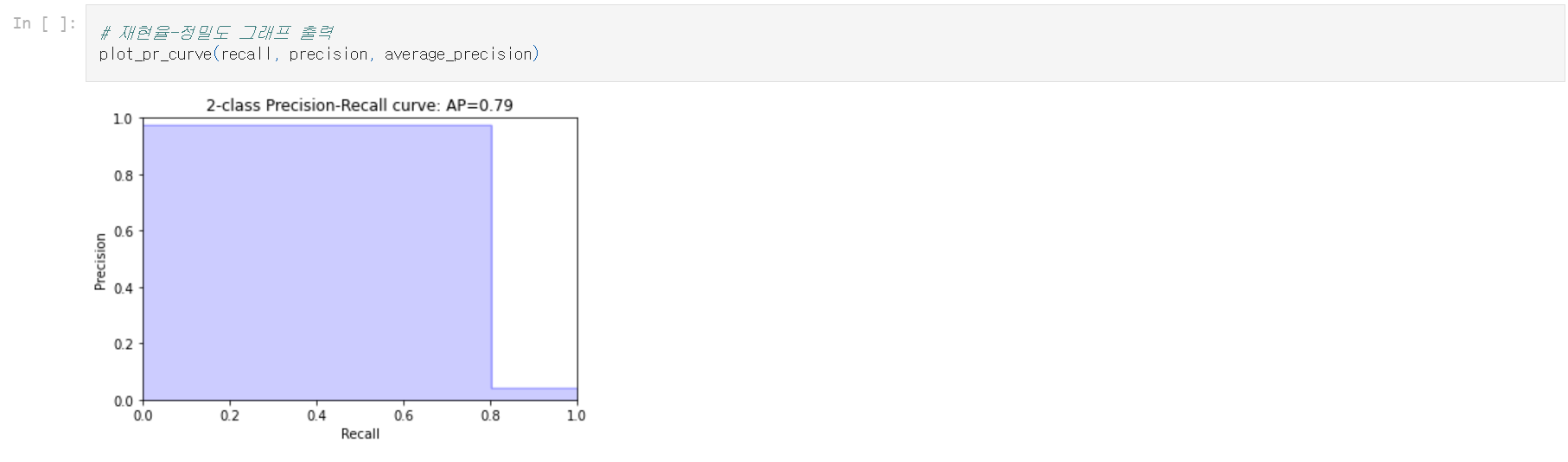
2.2.2 정밀도 대 재현율 시각화
정밀도-재현율 곡선을 시각화하여 둘 사이의 상호관계를 볼 수 있다. 정밀도가 증가하면 재현율이 떨어지고 그 반대의 경우도 마찬가지이다.
이 둘 사이의 균형을 달성해야 한다. 그렇지 않으면 많은 오탐지가 발생하거나 실제 부정거래 탐지가 충분하지 않을 수 있다.
이를 달성하고 성능을 비교하는 데에 정밀도-재현율 곡선이 유용하다. 사이킷런 패키지에서 평균 정밀도 점수와 PR 곡선을 간단히 얻을 수 있다.


2.3 알고리즘 가중치 조정하기
- 부정탐지에 최적화되도록 모델 매개변수를 조정
- 모델을 훈련시킬 때, 최상의 재현율-정밀도 트레이드오프를 얻기 위해 다양한 옵션과 설정을 시도
- 사이킷런은 매우 불균형한 데이터에 맞추어 모델을 변형시키기 위한 두 가지 간단한 옵션을 가짐
- class_weight:
- balanced mode
- balanced_subsample mode
- manual input
2.3.0.1 하이퍼파라미터 조정
- 랜덤 포레스트는 모델을 최적화하기 위한 많은 옵션을 가짐
model = RandomForestClassifier(n_estimators=10,
criterion=’gini’,
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
max_features=’auto’,
n_jobs=-1,
class_weight=None)- 랜덤 포레스트 내 트리들의 모양과 크기는 leaf size와 tree depth로 조절
- n_estimators: 가장 중요한 설정 중 하나는 나무의 수임
- max_features: 각 노드를 분할하는 데에 고려되는 특징의 수
- criterion: 각 노드에서 데이터가 분할되는 방법을 변경(기본값은 지니 계수)
2.3.0.2 GridSearchCV를 이용한 하이퍼파라미터 조정
GridSearchCV는 매개변수 그리드에 정의된 모든 매개변수의 조합을 평가함
# 매개변수 그리드 생성
param_grid = {'max_depth': [80, 90, 100, 110],
'max_features': [2, 3],
'min_samples_leaf': [3, 4, 5],
'min_samples_split': [8, 10, 12],
'n_estimators': [100, 200, 300, 1000]}
# 사용할 모델 정의
model = RandomForestRegressor()
# 그리드 서치 모델 초기화
grid_search_model = GridSearchCV(estimator = model,
param_grid = param_grid,
cv = 5,
n_jobs = -1,
scoring='f1')
GridSearchCV와 모델을 데이터에 적합시키면 best_params_ 속성으로 최적 모델의 매개변수를 얻을 수 있음
# 데이터에 적합시킴
grid_search_model.fit(X_train, y_train)
# 최적 매개변수 조합 획득
grid_search_model.best_params_
{'bootstrap': True,
'max_depth': 80,
'max_features': 3,
'min_samples_leaf': 5,
'min_samples_split': 12,
'n_estimators': 100}
GridSearchCV는 계산량이 많고 데이터 양과 매개변수의 수에 따라 많은 시간이 필요할 수 있음
2.3.1 모델 조정
class_weights 옵션을 사용함으로써 매우 불균형한 부정거래 데이터를 처리하기 위해 랜덤 포레스트 모델을 조정할 수 있다. 그러나 이는 약간 투박한 방법이며, 특정한 경우에는 작동하지 않을 수 있다.
여기에서는 Random Forest 모델의 weight = "balanced_subsample" 모드를 살펴본다.
- 분류기의 class_weight를 Balanced_subsample로 설정
- 모델을 훈련 세트에 적합시킴
- X_test에서 예측과 확률을 획득
- roc_auc_score, 분류 보고서 및 혼동 행렬 출력

결과가 크게 향상되지 않는다. FP가 줄어들었지만 이제 18개의 FN, 즉 탐지하지 못한 부정거래가 있다. 주로 부정거래를 잡는 데 관심이 있고 오탐지에 대해서 그다지 신경 쓰지 않는다면 시도할 수 있는 간단한 옵션이기는 하지만 실제로 모델을 전혀 개선해주지 않았다.
2.3.2 부정 탐지를 위해 랜덤 포레스트 모델 조정하기
여기에서는 가중치를 정하고 포레스트의 의사 결정 트리 모양을 조정하며 랜덤 포레스트 분류기의 옵션에 대해 알아보자. 불균형을 약간 상쇄할 수 있도록 가중치를 수동으로 정한다. 300건의 부정거래와 7000건의 정상거래가 있으므로 가중치 비율을 1:12로 설정하면 부정거래 3분의 1, 정상거래 3분의 2 비율이 되고, 이는 모델을 훈련하기에 충분하다.
- 가중치를 변경하여 부정거래 대 정상거래 비율을 1 대 12로 설정
- 분할 기준을 '엔트로피'로 설정
- 최대 깊이를 10으로 설정
- 노드의 최소 샘플을 10으로 설정
- 모델에서 사용할 나무의 수를 20으로 설정


더 많은 옵션을 잘 정하면 더 나은 예측을 얻을 수 있다. FN를 효과적으로 줄였다. 즉 FP를 낮게 유지하면서 더 많은 부정거래를 탐지하고 있다.
2.3.3 GridSearchCV를 이용한 매개변수 최적화
여기에서는 덜 무작위적인 방식으로, GridSearchCV를 사용하여 모델을 조정한다.
GridSearchCV를 사용하면 옵션에 점수를 매길 성능 항목을 정할 수 있다.
부정 탐지의 경우 가능한 한 많은 부정 사례를 잡는 데 주로 관심이 있으므로 가능한 높은 재현율을 얻도록 모델 설정을 최적화할 수 있다. FP를 줄이는 데 관심이 있다면 F1 점수로 최적화 할 수 있다.
- 매개변수 그리드를 정의함
- RandomForestClassifier를 정의하고 random_state를 5로 둠(모델 간 비교를 위함)
- 재현율을 최적화하도록 옵션 설정
- 모델을 X_train 및 y_train에 적합시키고 최적 매개변수를 획득

2.3.4 모델에 적용해 보기
분할 기준은 'gini', 트리 수는 30개, 최대 깊이는 8 등으로 설정되어야 함을 확인했으니 모델에 적용해 성능을 보자.
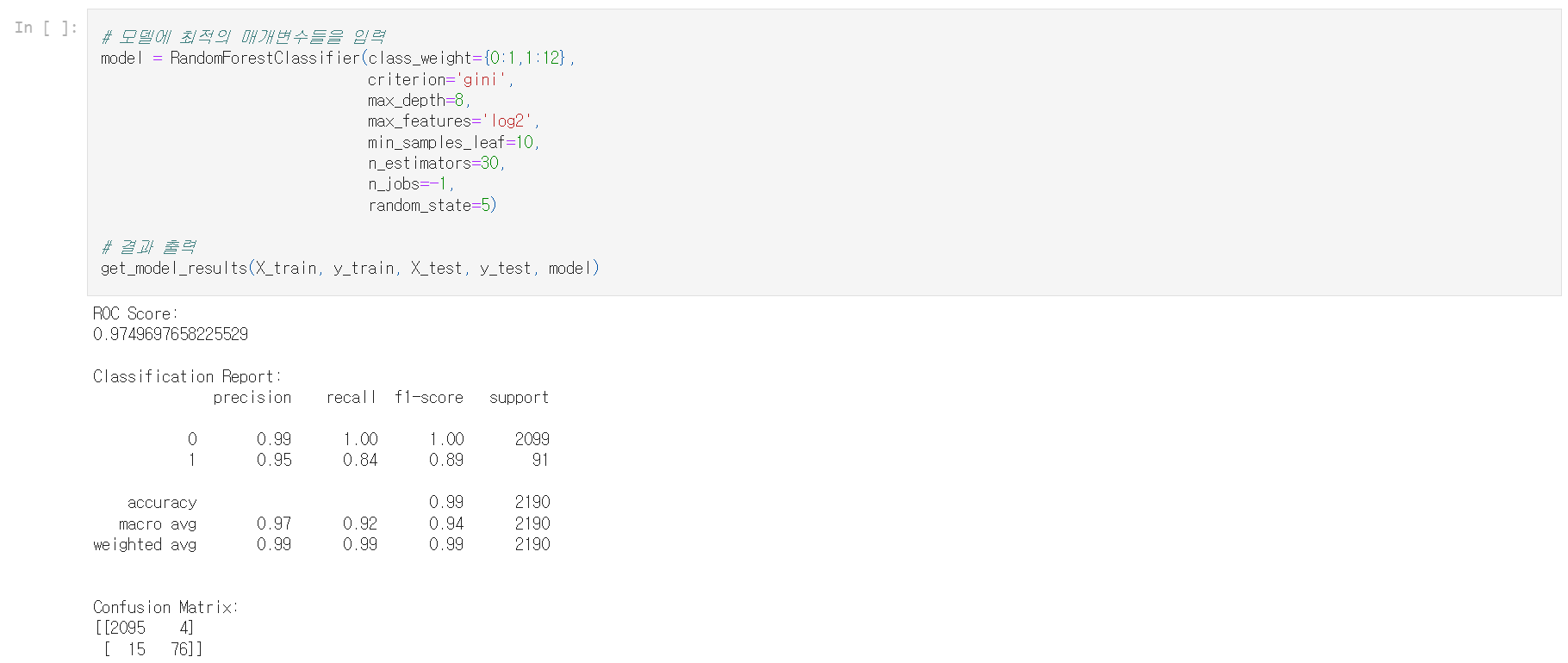
| ※ 원문에서는 여기에서 예측 결과가 개선되었다고 설명하고 있으나 수치를 보면 오히려 나빠지는 것으로 보인다. |
2.4. 앙상블 기법
- 앙상블 기법은 여러 머신러닝 모델을 만든 다음 이를 결합하여 최종 결과를 생성하는 기술
- 일반적으로 단일 모델보다 더 정확한 예측을 생성
- 머신러닝의 목표는 원하는 결과를 가장 잘 예측할 수 있는 단일 모델을 찾는 것
- 하나의 모델이 가장 정확한 예측기이기를 바라기보다는 앙상블 기법을 사용할 것 - 앙상블 기법은 수많은 모델을 고려하고 평균을 내서 하나의 최종 모델을 생성
- 강력한 예측을 보장
- 과적합 가능성이 적음
- 예측 성능을 향상(특히 재현율 및 정밀도 점수가 다른 모델들을 결합하여) - 랜덤 포레스트는 의사 결정 트리의 앙상블임(그림 참조)
- 부트스트랩 집계 또는 배깅 앙상블
- 데이터의 무작위 하위 샘플에 대해 훈련되고 모든 트리의 예측을 평균
2.4.0.1 앙상블 모델 쌓기
- 여러 모델은 모델 결과에 대한 투표 규칙을 통해 결합(그림 참조)
- 기본 수준 모델은 각각 완전한 훈련 세트를 기반으로 훈련됨(배깅 방법과 달리 데이터의 하위 샘플로 훈련되지 않음)
- 서로 다른 유형의 알고리즘 결합 가능
2.4.0.2 투표 분류기
- 사이킷런에서 사용 가능(앙상블 모델을 구현하는 쉬운 방법)
from sklearn.ensemble import VotingClassifier
# 모델 정의
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
# 모델 결합
ensemble_model = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')
# 다른 모델과 마찬가지로 훈련 데이터에 적합, 그리고 예측
ensemble_model.fit(X_train, y_train)
ensemble_model.predict(X_test)- Voting='hard' 옵션은 예측된 클래스 레이블을 사용하고 과반수 투표를 취함
- Voting='soft' 옵션은 개별 모델의 예측 확률을 결합하여 평균 확률을 취함
- 가중치를 VotingClassifer에 할당할 수 있음(weight=[2,1,1])
- 한 모델이 다른 모델의 성능을 크게 능가할 때 유용함
2.4.0.3 신뢰 가능한 레이블
- 실생활에서 데이터가 편향되지 않고 신뢰할 수 있는 레이블을 가질 가능성은 거의 없음
- 신용카드 데이터의 경우 신뢰할 수 있는 레이블이 있는 경우가 많으며, 이 경우 지금까지 배운 방법을 사용
- 부정탐지의 경우 대부분 비지도 학습에 의존해야 함
2.4.1 로지스틱 회귀
여기에서는 VotingClassifier를 사용하여 3개의 알고리즘을 하나의 모델로 결합한다. 이를 통해 모델들의 서로 다른 측면에서 이점을 얻을 수 있으며 전체 성능 개선하고 더 많은 부정 탐지를 기대할 수 있다.
첫 번째 모델인 로지스틱 회귀(Logistic Regression)은 최적의 Random Forest 모델보다 재현율이 약간 높지만 오탐지가 훨씬 더 많다. 가중치가 적용된 의사 결정 트리도 추가할 것이다.
투표 분류기가 모델을 개선할 수 있는지를 보려면 먼저 로지스틱 회귀 모델의 단독 실행 결과를 봐야 한다.
- 부정거래 클래스 가중치 1:15로 LogisticRegression 모델을 정의
- 모델을 훈련 세트에 적합시키고 예측을 실행한 뒤, 분류 보고서와 혼동 행렬을 출력

보다시피 로지스틱 회귀는 랜덤 포레스트와 성능이 상당히 다르다. 오탐지율이 더 높지만 재현율도 더 좋다. 따라서 앙상블 모델에서 랜덤 포레스트에 추가하기에 유용할 것이다.
2.4.2 투표 분류기
이제 3개의 모델을 하나로 결합하여 랜덤 포레스트 모델을 개선해 보자. 일반적인 랜덤 포레스트 모델과 앞에서 본 로지스틱 회귀를 간단한 의사 결정 트리와 결합할 것이다. get_model_results() 함수를 사용하여 앙상블 모델의 결과를 바로 볼 수 있다.
- 투표 분류기 패키지를 불러옴
- 세 가지 모델을 정의
- 3개의 분류기를 각각의 레이블과 함께 입력하여 앙상블 모델을 정의
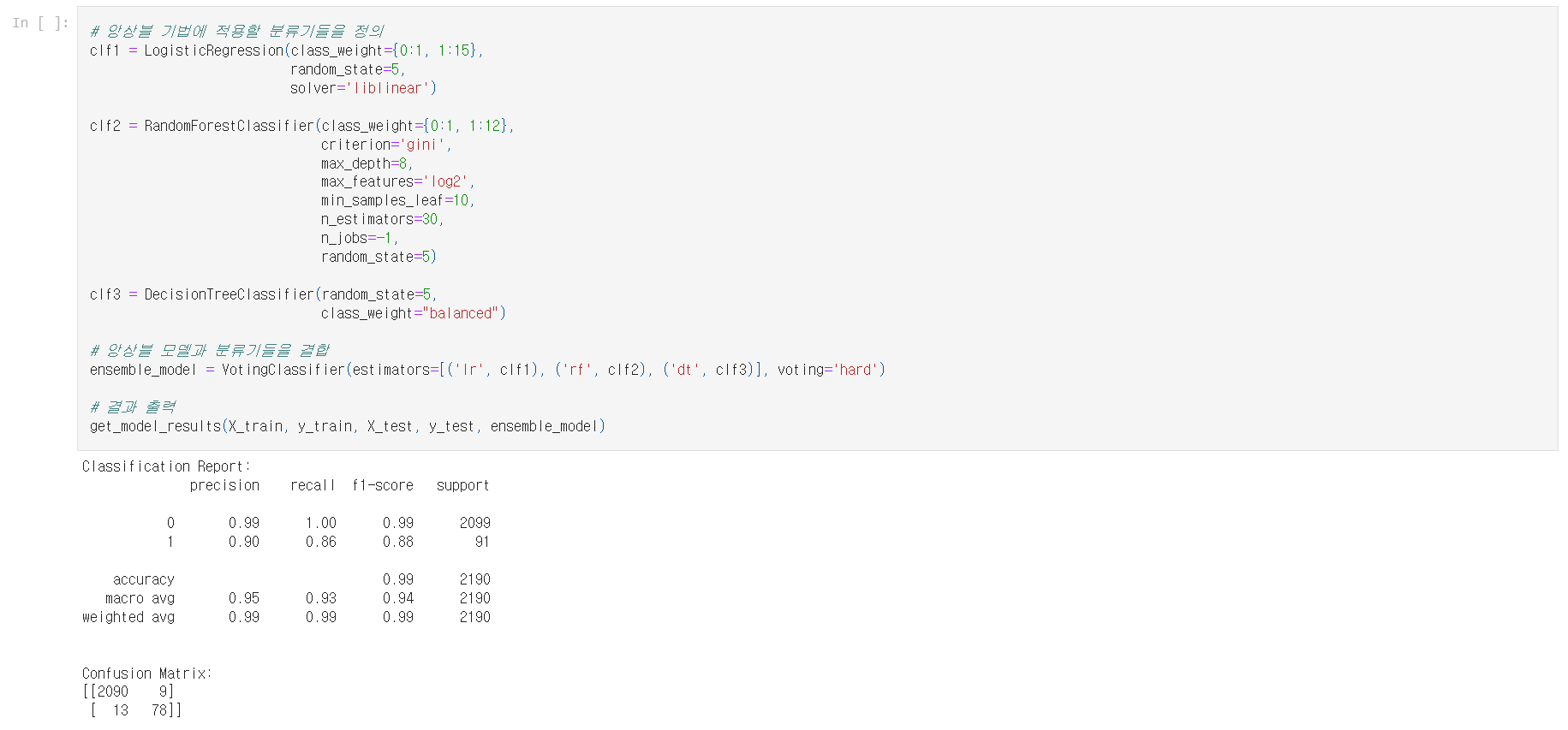
부정거래 탐지를 76건에서 78건으로 늘렸고 5건의 FP만 추가되었다. 오탐지를 낮게 유지하면서 가능한 한 많은 부정거래를 탐지하는 데 관심이 있다면 꽤 좋은 절충안이다. 로지스틱 회귀는 FP가 상당히 나빴고 랜덤 포레스트는 FN가 더 나빴다. 이를 결합함으로써 성능을 향상시킬 수 있었다.
2.4.3 투표 분류기 내에서의 가중치 조정
투표 분류기를 사용하면 성능을 향상시킬 수 있다는 것을 방금 확인했다. 이제 이 모델에 부여하는 가중치를 조정해 보자. 특정 모델이 나머지 모델보다 전반적으로 더 나은 성능을 갖고 있더라도 다른 모델과 결합하여 결과를 더욱 개선하려는 경우에 유용하다.
- 두 번째 분류기에 대해 4:1로 가중치를 주는 앙상블 모델을 정의
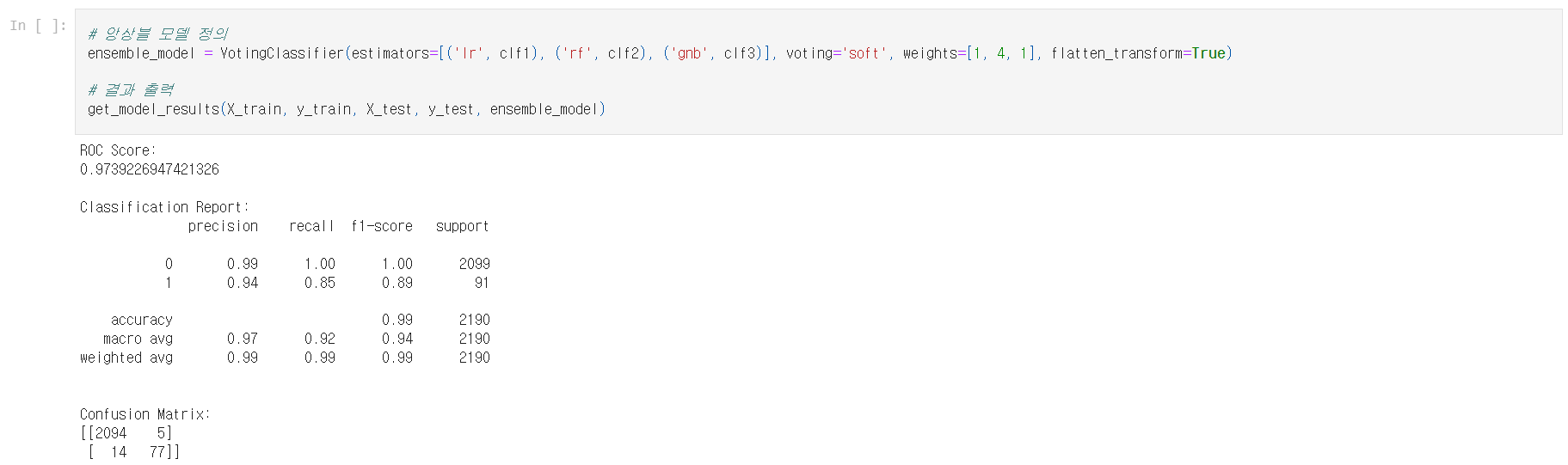
지도 학습을 이용한 부정거래 탐지를 살펴보았으니 다음으로는 레이블이 없을 때 부정거래를 탐지하는 방법(비지도 학습)을 살펴본다.
비지도 학습을 이용한 부정거래 탐지 부분은 파트 2/2로 별도 게시하였다.
파이썬과 사이킷럿(scikit-learn)을 이용한 머신러닝 예제/신용카드 부정 탐지(파트 2/2)
파이썬과 사이킷럿(scikit-learn)을 이용한 머신러닝 예제/신용카드 부정 탐지(파트 2/2)
신용카드 부정 탐지에 관한 머신러닝 예제를 아래 글에 이어서 계속 살펴보자. 파이썬과 사이킷럿(scikit-learn)을 이용한 머신러닝 예제/신용카드 부정 탐지(파트 1/2) 파이썬과 사이킷럿(scikit-learn)
codealone.tistory.com
'코딩 > 데이터분석(Pandas, ML, etc)' 카테고리의 다른 글
| 두 개의 판다스 데이터프레임에서 중복되지 않는 항목(차집합)만 걸러내는 방법 (1) | 2022.05.04 |
|---|---|
| 파이썬과 사이킷럿(scikit-learn)을 이용한 머신러닝 예제/신용카드 부정 탐지(파트 2/2) (0) | 2022.03.06 |
| 파이썬 머신러닝 라이브러리 Scikit-learn(사이킷런) 사용법 (0) | 2022.01.30 |
| 웹사이트(인터넷)에서 표를 판다스(Pandas) 데이터프레임으로 불러오는 방법/read_html (0) | 2021.12.27 |
| 판다스(Pandas)에서 시트가 여러 개인 엑셀 파일을 불러오는 방법 (0) | 2021.12.16 |




댓글